Breadth First Traversal in Graph

Graph Traversals

Traversing a graph is nothing but to visit or process all the nodes of the graph once and only once. two techniques are popular to traverse the graph. They are Breadth first traversal and depth first traversal. In both the traversal techniques the traversing starts from one of the nodes of the graph and from that starting node all other node are explored. In case of Breadth first traversal from the starting node all the adjacent nodes of that node are explored and the process of exploring is continued. In case of Depth first traversal only one adjacent node (from the adjacent nodes) is explored and the process of exploring continues. Understanding adjacent node is important in both the techniques of graph traversal.

Breadth First Traversal:

As the name of the traversal techniques suggests the traversal explores the nodes of graph by breadth. It means all the adjacent nodes of one selected node are explored first. From the start node all the adjacent nodes of that node are explored. From the list of explored nodes one of the node is selected as the next start node and the unexplored adjacent nodes of that node are explored. Then from the first list of explored nodes the second node is selected as the next start node and the unexplored adjacent nodes of that node are explored. The process continues till the exploration of all the nodes of the graph. The data structure QUEUE finds its application in this traversal. Consider the following graph:

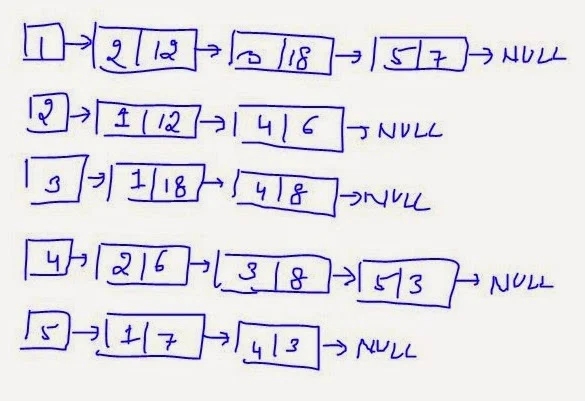
The adjacent nodes of the node

A     :     B     C     E

B     :     A     D

C     :     A     D

D     :     B     C     E

E     :     A     D 

The breadth first traversal of the above graph, assuming node 'A' as start node is:
A     B     C     E     D

You can observe from the traversal result that the first node visited is the starting node. Then the next nodes visited are the adjacent nodes of the start node 'A'. In the last 'D' is visited because it is the only unexplored adjacent node of 'B' the exploring of nodes may be in any order. So, the traversal may also be like:

A     C     B     E     D     OR

A     E     B     C     D.

If the start node is 'C' then the BFT (Breadth First Traversal) is:

C     A     D     B     E

The formal algorithm for the BFT is :

GRAPHBFT

[TA is the one dimensional array of size n where n is the number of nodes in the given graph]

Mark the start node and insert it in the QUEUE

Repeat while QUEUE is not empty

Delete QUEUE.
Add delete node to TA at the next position.
Mark the unmarked adjacent nodes of the deleted node.
Insert the marked nodes (if any) of the deleted node in the QUEUE.
[End of while]
Print TA from the first position as traversal.
Exit.

The above algorithm works in the following manner:

Consider the following graph



Let us assume the start node as node 'A'. Let us insert node 'A' in the QUEUE. So, the QUEUE is:

When QUEUE is deleted, the node obtained is 'A'. It is added to the traversed array. So, the traversed array is:

The marked adjacent nodes of deleted node 'A' are, B, C and E. Insert the nodes B, C and E in the QUEUE(in any order) So, the QUEUE is:

QUEUE is not Empty the process is repeated.
when QUEUE is deleted, the node obtained is 'B'. It is added to the traversed array. So, the traversed array is:

The marked adjacent nodes of deleted node 'B' is D. Insert the node D in the QUEUE so, the QUEUE is:

QUEUE is not empty the process is repeated.
When QUEUE is deleted, the node obtained is 'C'. It is added to the traversed array. So, the traversed array is:

The marked adjacent node of deleted node 'C' are none. So the QUEUE is:

QUEUE is not empty the process is repeated.
When QUEUE is deleted, the node obtained is 'E'. It is added to the traversed array. So, the traversed array is:

The marked adjacent node of deleted node 'E' are none. So, the QUEUE is:

QUEUE is not empty the process is repeated.
When QUEUE is deleted, the node obtained is 'D'. It is added to the traversed array. So, the traversed array is:

The marked adjacent nodes of deleted node 'E' are none. So, the QUEUE is:

The QUEUE is empty, stop the process.
When the array is printed we get the Breadth First Traversal as:
A     B     C     E     D

Handling Errors and Exceptions using Try-Catch: SQL

When you execute a query, it is parsed for syntactical errors before execution. If the syntax is correct, it is compiled and executed. Sometimes, due to factors, such as incorrect data, an error can occur during execution even if the query is syntactically correct. The errors that occur at run time are known as exceptions.

Consider an example. There is a primary key constraint applied on the EmployeeID attribute of the Employee table. When you try to insert an employee ID that already exists in the table, an error occurs while executing the INSERT statement.

When a database server provides database support to a business application, errors generated while executing the SQL statements can be handled in two ways:

• By adding error-handling code to the batch by using the TRY-CATCH construct.
• By returning the error to the business application by using the RAISERROR statement and handling the error in the application.

Using TRY-CATCH

A TRY-CATCH construct includes a TRY block followed by a CATCH block. A TRY block is a group of SQL statements enclosed in a batch, stored procedure, trigger, or function. If an error occurs in any statement of the TRY block, the control is passed to another group of statements that is enclosed in a CATCH block.

A CATCH block contains SQL statements that perform some operations when an error occurs. Therefore, an associated CATCH block must immediately follow a TRY block, as shown in the following syntax:

TRY
<SQL statements>
…
CATCH
<SQL statements>
…
END CATCH

If there are no errors in the code that is enclosed in a TRY block, the control is passed to the statement immediately after the associated END CATCH statement. In this case, statements enclosed in the CATCH block are not executed.

The TRY ……..CATCH constructs can be nested. Either a TRY block or a CTCH block can contain nested TRY…. CATCH constructs. A CATCH block can contain an embedded TRY… CATCH construct to handle errors encountered by the CATCH code.

In the CATCH block, you can use the following system functions to determine information about the errors:
ERROR_LINE0: returns the line number at which the error occurred.

• ERROR_MESSAGE0: specifies the text of the message that would be returned to the application. The text includes the values supplied for any substitutable parameters, such as lengths, object names, or times.
• ERROR_NUMBER0: returns the error number.
• ERROR_PROCEDURE0: returns the name of the stored procedure or trigger in which the error occurred. This function returns NULL if the error did not occur within a stored procedure or trigger.
• ERROR_SEVERITY0: returns the severity.
• ERROR_STATE0: returns the state of the error.

Consider an example. The EmployeeID attribute of the Employee table in the Adventure Works database is an IDENTITY column and its value cannot be specified while inserting a new record. In this case, if you specify the value for the EmployeeID in the INSERT statement, an error will be generated.

To handle such run-time errors, you can include the insert statement in a TRY block and send the control to the following CATCH block where the error information is displayed, as shown in the following statements:

BEGIN TRY
INSERT INTO [AdventureWorks] . [Person] . [Contact]
VALUES (0, null, ‘Robert’, ‘J’ , ‘Langdon’, NULL, ‘rbl@adventure-works.com’, 0, ‘1 (11) 500 555-0172’, ‘9E685955-ACD0-4218-AD7F-60DDF224C452’, ‘2a31OEw=’, NULL, newid( ), getdate ( ))

INSERT INTO [AdventureWorks] . [HumanREsources] . [Employee]
VALUES (‘AS01AS25R2E365W’, 19979, ‘robert1’, 16, ‘Tool Designer’, ‘1972-05-15’, ‘S’, ‘M’, ‘1996+-07-31’, 0, 16, 20, 1, newid( ), getdate ( ))

Adjacency List Representation in Graph

In case of adjacency list representation 'n' number of singly linked lists are used to represent a graph of 'n' number of nodes. The adjacent nodes are represented as nodes of the individual linked lists representing each node (vertex). If there are no adjacent nodes then the linked list of the respective vertex point to NULL. Consider the following undirected graph:

The adjacency list representation is:

In the above adjacency list representation the external pointer '1' contains the address of the first adjacent node of node 1 of graph. The linked list is the adjacency list of node 1. The first node of the list contains the address of second adjacent node 4. Similarly the node 4 contains the address of the last adjacent node of node 1 i.e. node 6. The link of the last node points to NULL. In this way the linked lists are created for all the vertices (nodes) of the graph. Consider the following digraph:

The adjacency list of the above digraph is:

Consider the following weighted graph:

The adjacency list of above weighted graph is:

In the above adjacency lists one extra part of the node is used to store the weight of the connecting edge. The other parts are used as usual one for node number or label and the other for the address of next node.

Adjacency matrix representation in Graph

Pictorially it is very the graph can be represented very easily and analysis can be done quite normally. But there is no direct pictorial data structure available to represent the graph. The basic data structure serve the purpose to store the graph in the memory. The data structures two-dimensional array and linked list most commonly used to represent the graphs. If the graph is represented using two dimensional array then the representational is called as "adjacency matrix representation" and if the linked list is used to represent the graph then the representation is called as "adjacency list representation".

Adjacency Matrix Representation:

A two dimensional array of size nxn can be used to represent the graph where 'n' is the number of vertices of the graph. 'n' number of rows are used to represent the vertices and 'n' number of columns are used for each vertex. The matrix entries depend on the type of graph. If the graph is undirected or directed then each row for the respective vertex contains the number of direct paths to each vertex is entered in the matrix. If the graph is weighted graph then the matrix entries for each row will be the weight of the edge to other vertices is entered as matrix entry. Consider the following undirected graph:

In the given graph, the node 2, 4 and 6 are adjacent to 1(there exist a direct path). So, in the adjacency matrix the row entry for vertex 1 contains '1' for each column representing vertices 2, 4 and 6 and rest of the entries will be 0 for that row. Similarly the row for vertex 2 contains entry '1' for column 1 and 5, '0' for 2, 4 and 6. You can note that 1 and 5 are adjacent nodes of vertex 2. In our all discussions node and vertex are synonyms. The complete adjacency matrix is:

In the above adjacency matrix each row is used for each node and each column is used for each node. Adj ij entry will be 1 if node 'i' is adjacent to 'j' otherwise it is 0 where 'Adj' is adjacency matrix, 'i' represents rows for nodes 1,2,3,4,5,6 and 'j' represents columns for nodes 1,2,4,5,6.

Consider the following digraph:

Nodes 2 and 6 are adjacent nodes of 1. Node 5 is the only adjacent node of 2. Nodes 1 and 5 are adjacent node 4. Node 6 is the adjacent node of 5. There are no adjacent nodes of node 6 it means it is not possible to move from node 6 to any other nodes of the graph (no direct path). So, the adjacency matrix is:

The adjacency matrix of a directed graph is not always symmetric whereas the adjacency matrix of an undirected graph is always symmetric. So, determination of only upper triangle of the adjacency matrix is more than enough for an undirected graph.

Consider the following weighted graph:

In the adjacency matrix of the above weighted graph the entries are the respective weight of the edges of the adjacent nodes if any exists otherwise it will be '∞' (unknown weight). So, the adjacency matrix is:

How to use Case and While statement in Batches: SQL

Database developer can use the CASE as well as While statement in situation where several conditions need to be evaluated.

Using CASE statement

The CASE statement evaluates a list of conditions and returns one of the possible results. You can use the IF statement to do the same task. However, you can use a CASE statement when there are more than two conditions that check a common variable for different values. The syntax of the CASE statement is:

CASE
WHEN Boolean_expression THEN expression
[ [WHEN Boolean_expression THEN expression] […..] ]
[ELSE expression]
END
Where,

• Boolean_expression specifies a bollean expression that is evaluated when using the CASE construct.
• Expression is the resultant expression that is executed when the Boolean expression evaluates to TRUE. This can be a constant, a column name, a function, a query, or any combination of arithmetic, bit-wise, and string operators.

In a simple CASE construct, a variable or an expression is compared with the Boolean expression in each WHEN clause. If any of these expressions evaluate to TRUE, then the expression specified with the THEN clause is executed. If the expression does not evaluate to TRUE, the expression with the ELSE statement is executed.

Consider the following example where a case construct is included in the SELECT statement to display the marital status as ‘Married’ or Single’:

SELECT EmployeeID, ‘Marital status’ =
CASE MaritalStatus
WHEN ‘M’ THEN ‘Married’
WHEN ‘S’ THEN ‘Single’
ELSE ‘Not specified’
END
FROM HumanResources.Employee
GO

Using the While Statement

You can use the WHILE statement in a batch to allow a set of T-SQL statement to execute repeatedly as long as the given condition holds true. The syntax of the WHILE statement is:

WHILE Boolean_expression
{sql_statement | statement_block}
[BREAK]
{sql_statement | statement_block}
[CONTINUE]
Where,

• Boolean_expression is an expression that evaluates to TRUE or FALSE.
• Sql_statement is any SQL statement.
• Statement_block is a group of SQL statements.
• BREAK causes the control to exit from the WHILE loop.
• CONTINUE causes the WHILE loop to restart, skipping all the statements after the CONTINUE keyword.

The SQL Server provides the BREAK and CONTINUE statements to control the statement within the WHILE loop. The BREAK statement causes an exit from the WHILE loop. Any statements that appear after the END keyword, which marks the end of the loop, are executed after the BREAK statement is executed. The CONTINUE statement causes the WHILE loop to restart, skipping any statements after this statement inside the loop.

Consider the following example where the HR department of AdventureWorks, Inc. has decided to review the salary of all the employees. As per the current HR policy, the average hourly salary rate of all the employees should be approximately $20. You need to increase the hourly salary of all the employees until the average hourly salary reaches near $20. In addition, you need to ensure that the maximum hourly salary should not exceed $127.

WHILE (SELECT AVG(Rate) +1 FROM HumanResources.EmployeePayHistory) <20
BEGIN
UPDATE HumanResources.EmployeePayHIstory
SET Rate = Rate +1
FROM HumanResources.EmployeePayHistory
IF (SELECT max (Rate) +1 FROM
HumanResources.EmployeePayHistory)>127
BREAK
ELSE
CONTINUE
END

How to use Constructs in Batches for Conditional Execution: SQL

SQL Server allows you to use programming constructs in the batches for conditional execution of statements. For example, you need to retrieve data based on a condition. If the condition is not satisfied, a message should be displayed.

The SQL Server allows you to use the following constructs to control the flow of statements:

• IF…..ELSE statement
• CASE statement
• WHILE statement

Using the IF….ELSE Statement

You can use the IF…..ELSE statement for conditional execution of SQL statements. A particular action is performed when the given condition on evaluates to TRUE and another action is performed when the given condition evaluates to FALSE.
The syntax of IF….ELSE statement is:

IF Boolean_expression
{sql_statement | statement_block}
ELSE
{sql_statement | statement_block}]
Where,

• Boolean_expression specifies the condition that evaluates to either TRUE or FALSE. Sql_statement specifies a T-SQL statement.
• Statement_block is a collection of T-SQL statements.

The following example retrieves the pay rate of an employee from the EmployeePayHistory table to a variable, @Rate. The value of the @Rate variable is compared with the value 15 by using the <(less than) comparison operator. Based on the condition, different messages are displayed.

DECLARE @Rate money
SELECT @Rate = Rate FROM HumanResources.EmployeeHistory
WHERE EmployeeID = 23
IF @Rate < 15
PRINT ‘Review of the rate is required’
ELSE
BEGIN
PRINT ‘Review of the rate is not required’
PRINT ‘Rate =’
PRINT @Rate
END
GO

In the preceding example, the IF statement checks if the rate variable is storing a value less than 15. If the result is true, the PRINT statement displays “Review of the rate is required” else it displays “Review of the rate is not required”. Further, the next PRN statement displays the value of the rate.

Consider another example, where a check is performed to see the existence of the sales department. If the Sales department exists, all the details are displayed otherwise, a user-defined message is displayed.

IF EXISTS (SELECT * FROM HumanResources.Department WHERE Name = ‘Sales’)
BEGIN
SELECT * FROM HumanResources.Department WHERE Name = ‘Sales’
END
ELSE
PRINT ‘Department details not available’
GO

How to Change Default Behaviour of element in jQuery

Earlier article was about installing and embedding jQuery on our web-pages, and then using jQuery selectors to perform some events. These events can be easily written on the same page or may be in another javascript file having extension (js).

jQuery provides simple function to prevent the default behavior of any event on the web page. I have an anchor tag on the page and on the click on that tag I am redirecting the user on the jQuery.com website.

Now to cancel this redirection programmer can use:

$( document ).ready(function() {
    $( "a" ).click(function( event ) {
               event.preventDefault();
    });
});

The above code will can cancel all the redirection of all the anchor tag on the page. If you want to prevent the behavior for some specific element then use their id or may be class selector. Selectors have discussed in earlier article, you can get more help out there.

Let’s suppose we have a form filling out all the details by the user and at the last there is a submit button to post the form data to controller. Now we don’t want to post data then we can use this simple jQuery code:

$( document ).ready(function() {
    $( "#btnSubmit" ).click(function( event ) {
               event.preventDefault();
    });
});

Now we have some more buttons or may be anchor tag to be used on the form but don’t want their click event or redirection on their click. Add any class for each of the anchor element whichever click event you want to cancel and write the following code:

$( document ).ready(function() {
    $( ".className" ).click(function( event ) {
               event.preventDefault();
    });
});

Selectors in jQuery