In case of adjacency list representation 'n' number of singly linked lists are used to represent a graph of 'n' number of nodes. The adjacent nodes are represented as nodes of the individual linked lists representing each node (vertex). If there are no adjacent nodes then the linked list of the respective vertex point to NULL. Consider the following undirected graph:
In the above adjacency list representation the external pointer '1' contains the address of the first adjacent node of node 1 of graph. The linked list is the adjacency list of node 1. The first node of the list contains the address of second adjacent node 4. Similarly the node 4 contains the address of the last adjacent node of node 1 i.e. node 6. The link of the last node points to NULL. In this way the linked lists are created for all the vertices (nodes) of the graph. Consider the following digraph:
The adjacency list of the above digraph is:
Consider the following weighted graph:
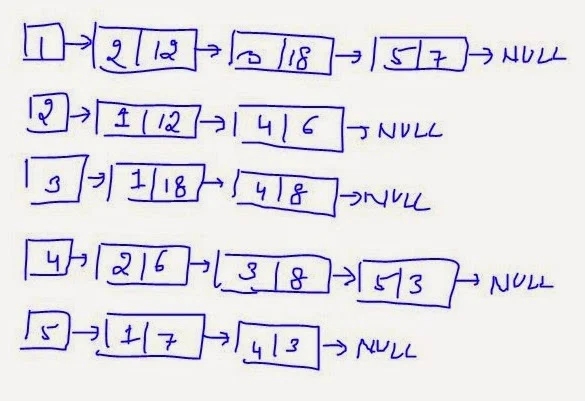
The adjacency list of above weighted graph is:
In the above adjacency lists one extra part of the node is used to store the weight of the connecting edge. The other parts are used as usual one for node number or label and the other for the address of next node.
The adjacency list representation is:
In the above adjacency list representation the external pointer '1' contains the address of the first adjacent node of node 1 of graph. The linked list is the adjacency list of node 1. The first node of the list contains the address of second adjacent node 4. Similarly the node 4 contains the address of the last adjacent node of node 1 i.e. node 6. The link of the last node points to NULL. In this way the linked lists are created for all the vertices (nodes) of the graph. Consider the following digraph:
The adjacency list of the above digraph is:
Consider the following weighted graph:
The adjacency list of above weighted graph is:
In the above adjacency lists one extra part of the node is used to store the weight of the connecting edge. The other parts are used as usual one for node number or label and the other for the address of next node.