I want to show Components in a tabs , so first of all create few components. In this project we have three components, First View Component public class AllViewComponent : ViewComponent { private readonly UserManager<ApplicationUser> _userManager; public AllViewComponent(UserManager<ApplicationUser> userManager) { _userManager = userManager; } public async Task<IViewComponentResult> InvokeAsync() { List<StudentViewModel> allUsers = new List<StudentViewModel>(); var items = await _userManager.Users.ToListAsync(); foreach (var item in items) { allUsers.Add(new StudentViewModel {Id=item.Id, EnrollmentNo = item.EnrollmentNo, FatherName = item.FatherName, Name = item.Name, Age = item.Age, Birthdate = item.Birthdate, Address = item.Address, Gender = item.Gender, Email = item.Email }); }
Graph is a non-linear data structure which is a collection of nodes also called as vertices and edges also called as arcs. So, if 'G' is a Graph mathematically it is represented as, G=(V,E) where 'V' is the non empty set of vertices 'E' is the set of edges. The edge if it exists in the graph connects any two nodes only. There may be more than one edge connecting the same nodes. If the edges in a graph show direction then such edges are called as directed edges and the graphs containing such directed edges are called as directed graphs or simply digraphs. If the graph contains undirected edges (represented by straight lines) then it is called as undirected graph or simply graph.
Set of vertices, V={A,B,C,D,E,F,G}
Set of edges, E={AB,AD,AF,BC, CE, DE, EG, FG}
In undirected graph the edge AB is similar to BA. Only one representation is considered. But in a directed graph the edge AB means, the edge starts from A and ends in B.
Directed Graph or digraph:
Set of vertices, V={A,B,C,D,E,F,G}
Set of edges, E={AB,AD,CB,DE,EC,EG,FG,FA}
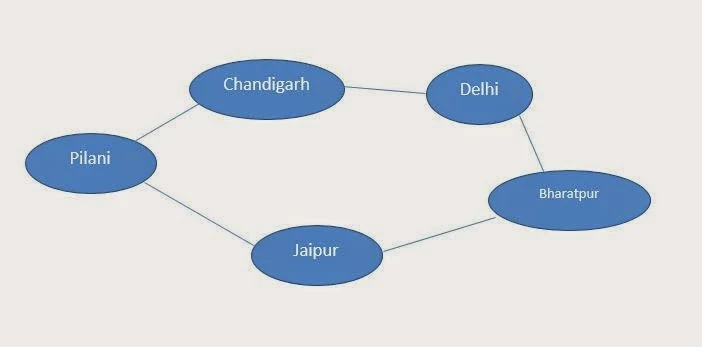
Scenario: A person moves from pilani to Jaipur by road. From Jaipur he reaches Delhi via Bharatpur. The person comes back to pilani via chandigrah.
How many places the person has visited? How much distance he has covered? How much time he takes to make a tip?
To answer all these questions it is necessary to go through the scenario many a times. If the same scenario is represented pictorially then answering the questions will be very easy. That is what the major benefit of graph is. See the following representation.
The above representation is a graph from which we can instantly say the person visited 4 places from pilani. If we mark the edges by means of either distance or time required to reach then the graph becomes weighted graph. See the following graph where the edges are marked with distances in kilometers.
From the above weighted graph we can easily say that the person has traveled 710 kilometers. If the edges are labeled with time as weight we can easily calculate the time required to cover the places. In the above graph there exists route from Pilani to Jaipur then vice-versa is also true. So, in undirected graph an edge is a two-way edge. But in case of digraph the edge if exists represents one-way.
Consider the following undirected graph:
Set of vertices, V={1,2,3,4,5,6}
Set of edges, E={12,14,16,23,35,45,56}, Number of edges=7
Degree of any vertex is total number of incident edges. So, in the graph degree of vertex 1 is 3, 2 is 2, 3 is 2, 4 is 2, 5 is 3 and vertex 6 is 2. Sum of degree of all vertices of graph is 14. The sum is always even. Number of edges in the graph is equal to 7. Therefore we can derive a relation between number of edges in a graph and sum of degree of vertices of graph. The relation is:
Number of edges in graph = 1/2 (Sum of degree of vertices)
where m is number of edges of a graph, d(Vi )The same relation holds true for digraph also. In a digraph degree of a vertex is equal to sum of in degree and out degree.
In degree of a vertex is equal total number of edges entering into the vertex and out degree is equal to total number of edges going out of the vertex.
In the above graph there exists an edge from vertex 1 to 2. There is no direct edge existing from 1 to 3. But it is possible to move to 3 from 1 via 2. It is called as path. In a directed graph if the path terminates in a start node then it is cycle. There are 3 paths from node 1 to node 5. They are 1-2-3-5, 1-4-5 and 1-6-5. The path 1-2-3-5 is a collection of paths 1-2, 2-3 and 3-5. In a graph if two nodes are directly connected then there exists a direct path. If there exists an edge from one vertex 'i' to other vertex 'j' then node 'i' and 'j' are called as adjacent nodes. From the above graph we can list the adjacent nodes of each vertex as:
Comments
Post a Comment